树链剖分

简单回顾一下树链剖分（以下摘自2009年漆子超的论文《分治算法在树的路径问题中的应用 》）：

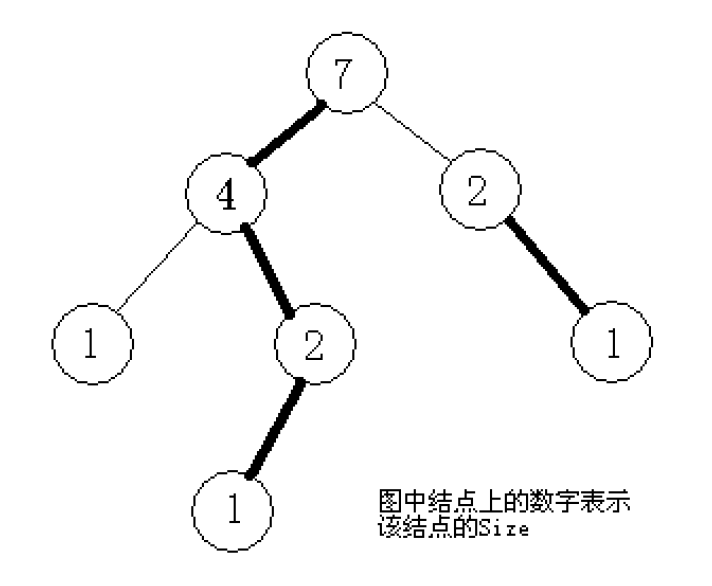
定义：

• 将树中的边分为两类：轻边和重边。
• 记$Size(U)$表示以$U$为根的子树的结点个数。
• 令$V$为$U$的儿子中$Size(V)$最大的一个，那么我们称边$(U,V)$为重边，其余边为轻边。
• 我们称某条路径为重路径，当且仅当它全部由重边组成。

性质：

• 性质1：如果$(U,V)$为轻边，则$Size(V) \leq \frac{Size(U)}{2}$。
• 性质2：从根到某一点的路径上轻边的个数不大于$O(log_{2} N)$。
• 性质3：我们称某条路径为重路径，当且仅当它全部由重边组成。那
  么对于每个点到根的路径上都不超过 $O(log_{2} N)$ 条轻边和
  $O( log_{2} N)$条重路径。

证明：

性质1根据定义来看比较显然。

性质2的话，从某点出发向上走，每经过一条轻边，当前子树的大小就至少变成2倍（由性质1得），所以根到某一点的路径上轻边的个数不大于$O(log_{2} N)$。

性质3，因为重路径是被轻边间隔开的，所以从每个点到根的路径上经过的重路径的条数是不超过轻边条数+1的，所以也是$O( log_{2} N)$级别的。

应用：

• 用于求LCA（推荐）
• 与线段树结合维护查询树链信息
• 利用重链dfs序连续，代替倍增求点x往上跳k步的点是谁。

代码：

• deep数组表示深度
• fa数组表示父节点
• son数组表示重儿子
• top数组表示每个点所在重链的顶端节点
• pos数组表示每个点按照重链优先dfs下的dfs序

int deep[N],fa[N],num[N],son[N],top[N],pos[N];
void dfs(int x,int pre,int d) {
    deep[x]=d;
    fa[x]=pre;
    num[x]=1;
    for(auto &y:e[x])
        if(y!=pre) {
            dfs(y,x,d+1);
            num[x]+=num[y];
            if(son[x]==-1 || num[y]>num[son[x]])
                son[x]=y;
        }
}
void dfs(int x,int root) {
    top[x]=root;
    pos[x]=++cnt;
    if(son[x]==-1) return;
    else dfs(son[x],root);
    for(auto &y:e[x])
        if(y!=fa[x] && y!=son[x])
            dfs(y,y);
}
int getmax(int x,int y) { //求树链点权最大值
    int f1=top[x],f2=top[y];
    int ans=-inf;
    while(f1!=f2) {
        if(deep[f1]<deep[f2]) {
            swap(x,y);
            swap(f1,f2);
        }
        ans=max(ans,ask_max(1,pos[f1],pos[x])); //ask_max 线段树查询
        x=fa[f1];
        f1=top[x];
    }
    if(deep[x]>deep[y]) swap(x,y);
    return max(ans,ask_max(1,pos[x],pos[y]));
}
void init() {
    memset(son,-1,sizeof(son));
    cnt=0;
}