写在前面 推荐hihocoder 上的讲解,可以说是十分清楚了。
用好后缀自动机不是十分容易,但看完本文的总结应该能至少达到签到水平…
正文
后缀自动机(Suffix Automaton,简称SAM)。对于一个字符串S,它对应的后缀自动机是一个最小的确定有限状态自动机(DFA),接受且只接受S的后缀。
先给出一张图和一个表格。
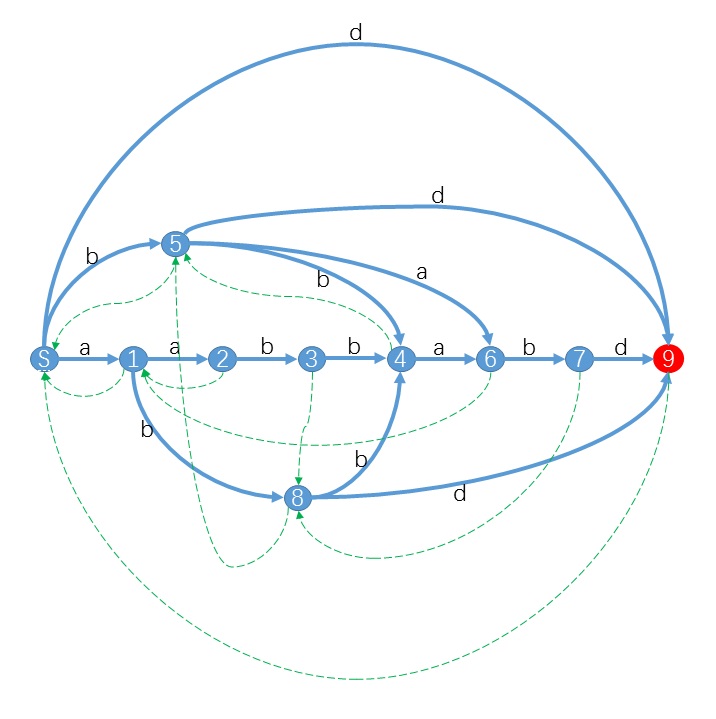
对于字符串STR=“aabbabd”,它的后缀自动机是:
状态
子串
endpos
S
空串
{0,1,2,3,4,5,6}
1
a
{1,2,5}
2
aa
{2}
3
aab
{3}
4
aabb,abb,bb
{4}
5
b
{3,4,6}
6
aabba,abba,bba,ba
{5}
7
aabbab,abbab,bbab,bab
{6}
8
ab
{3,6}
9
aabbabd,abbabd,bbabd,babd,abd,bd,d
{7}
接下来从状态(State)、转移函数(Transition Function)、后缀链接(Suffix Link)三个方面全方位了解一下后缀自动机的性质。
状态:
记号:
l e n g t h ( s ) length(s) l e n g t h ( s ) s s s e n d p o s ( s ) endpos(s) e n d p o s ( s ) s s s S T R STR S T R s u b s t r i n g s ( s t ) substrings(st) s u b s t r i n g s ( s t ) s t st s t l o n g e s t ( s t ) longest(st) l o n g e s t ( s t ) s t st s t s h o r t e s t ( s t ) shortest(st) s h o r t e s t ( s t ) s t st s t m a x l e n ( s t ) = l e n g t h ( l o n g e s t ( s t ) ) maxlen(st)=length(longest(st)) m a x l e n ( s t ) = l e n g t h ( l o n g e s t ( s t ) )
性质:
从起始状态 S S S S T R STR S T R
对于 S T R STR S T R s 1 s_1 s 1 s 2 s_2 s 2 l e n g t h ( s 1 ) ≤ l e n g t h ( s 2 ) length(s_1) \leq length(s_2) l e n g t h ( s 1 ) ≤ l e n g t h ( s 2 ) s 1 s_1 s 1 s 2 s_2 s 2 e n d p o s ( s 2 ) ⊆ e n d p o s ( s 1 ) endpos(s_2) \subseteq endpos(s_1) e n d p o s ( s 2 ) ⊆ e n d p o s ( s 1 ) s 1 s_1 s 1 s 2 s_2 s 2 e n d p o s ( s 1 ) ⋂ e n d p o s ( s 2 ) = ∅ endpos(s_1) \bigcap endpos(s_2) = \emptyset e n d p o s ( s 1 ) ⋂ e n d p o s ( s 2 ) = ∅
对于一个后缀自动机的状态 s t st s t s u b s t r i n g s ( s t ) substrings(st) s u b s t r i n g s ( s t ) e n d p o s endpos e n d p o s e n d p o s ( s t ) endpos(st) e n d p o s ( s t ) e n d p o s endpos e n d p o s
对于一个后缀自动机的状态 s t st s t s ∈ s u b s t r i n g s ( s t ) s \in substrings(st) s ∈ s u b s t r i n g s ( s t ) s s s l o n g e s t ( s t ) longest(st) l o n g e s t ( s t )
对于一个状态 s t st s t l o n g e s t ( s t ) longest(st) l o n g e s t ( s t ) s s s s s s l e n g t h ( s h o r t e s t ( s t ) ) ≤ l e n g t h ( s ) ≤ l e n g t h ( l o n g s e s t ( s t ) ) length(shortest(st)) \leq length(s) \leq length(longsest(st)) l e n g t h ( s h o r t e s t ( s t ) ) ≤ l e n g t h ( s ) ≤ l e n g t h ( l o n g s e s t ( s t ) ) s ∈ s u b s t r i n g s ( s t ) s \in substrings(st) s ∈ s u b s t r i n g s ( s t )
换句话说,s u b s t r i n g s ( s t ) substrings(st) s u b s t r i n g s ( s t ) l o n g e s t ( s t ) longest(st) l o n g e s t ( s t )
转移函数:
记字符集合n e x t ( s t ) next(st) n e x t ( s t ) s t st s t n e x t ( s t ) = S T R [ i + 1 ] ∣ i ∈ e n d p o s ( s t ) next(st) = {STR[i+1] \mid i \in endpos(st)} n e x t ( s t ) = S T R [ i + 1 ] ∣ i ∈ e n d p o s ( s t ) s t st s t n e x t ( s t ) next(st) n e x t ( s t ) s u b s t r i n g s ( s t ) substrings(st) s u b s t r i n g s ( s t ) n e x t ( 4 ) = a next(4)={a} n e x t ( 4 ) = a
定义转移函数 t r a n s ( s t , c ) = x ∣ l o n g e s t ( s t ) + c ∈ s u b s t r i n g s ( x ) trans(st, c) = x \mid longest(st) + c \in substrings(x) t r a n s ( s t , c ) = x ∣ l o n g e s t ( s t ) + c ∈ s u b s t r i n g s ( x ) l o n g e s t ( s t ) longest(st) l o n g e s t ( s t ) s s s s s s x x x t r a n s ( s t , c ) trans(st, c) t r a n s ( s t , c ) x x x
对应图中蓝线,比如 t r a n s ( 4 , a ) = 6 trans(4, a)=6 t r a n s ( 4 , a ) = 6
后缀链接:
前面我们讲到s u b s t r i n g s ( s t ) substrings(st) s u b s t r i n g s ( s t ) l o n g e s t ( s t ) longest(st) l o n g e s t ( s t ) e n d p o s endpos e n d p o s e n d p o s endpos e n d p o s e n d p o s endpos e n d p o s e n d p o s endpos e n d p o s
于是我们可以发现一条状态序列:7->8->5->S。这个序列的意义是 l o n g e s t ( 7 ) longest(7) l o n g e s t ( 7 )
后缀链接组成了一棵以S为根的树。
构造后缀自动机:
构造比较复杂,还是推荐看 http://hihocoder.com/contest/hiho128/problem/1
具体改天再写 ~
时间复杂度 O ( N ) O(N) O ( N ) 2 N 2N 2 N
代码中 son 表示转移函数,pre 表示后缀链接,cnt 表示 e n d p o s endpos e n d p o s
添加字符的过程中只能标出 e n d p o s endpos e n d p o s 1 1 1 e n d p o s endpos e n d p o s
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 #include <bits/stdc++.h> using namespace std;#define N 1000010 struct SAM { int tot,last; int son[N<<1 ][26 ],maxlen[N<<1 ],pre[N<<1 ]; int cnt[N<<1 ],in[N<<1 ],q[N<<1 ]; void init () { tot=0 ; last=newnode (); } int newnode () { ++tot; memset (son[tot],0 ,sizeof (son[tot])); maxlen[tot]=pre[tot]=cnt[tot]=in[tot]=0 ; return tot; } void add (int c) { int now=newnode (); maxlen[now]=maxlen[last]+1 ; cnt[now]=1 ; while (last && son[last][c]==0 ) son[last][c]=now,last=pre[last]; if (last) { int x=son[last][c]; if (maxlen[x]==maxlen[last]+1 ) pre[now]=x; else { int nq=newnode (); maxlen[nq]=maxlen[last]+1 ; memcpy (son[nq],son[x],sizeof (son[x])); pre[nq]=pre[x]; pre[x]=pre[now]=nq; while (last && son[last][c]==x) son[last][c]=nq,last=pre[last]; } } else pre[now]=1 ; last=now; } void endpos () { int l=0 ,r=0 ; for (int i=1 ;i<=tot;++i) ++in[pre[i]]; for (int i=1 ;i<=tot;++i) if (!in[i]) q[r++]=i; while (l!=r) { int x=q[l++]; if (pre[x]==0 ) continue ; cnt[pre[x]]+=cnt[x]; if ((--in[pre[x]])==0 ) q[r++]=pre[x]; } } } sam; char s[N];int main () sam.init (); scanf ("%s" ,s); for (int i=0 ;s[i];++i) sam.add (s[i]-'a' ); sam.endpos (); }
广义后缀自动机
解决多个串的问题,做法很简单,只需要添加每个串前让last=1即可,或者也可以对trie树建后缀自动机,则新加点时last为trie上的父节点。分析与证明在2015年国家集训队论文里有。
如果要记录一些信息,比如strval表示每个状态里的子串在多少个串中出现过,需要额外加一个lc维护该状态上一次出现是哪个串,每次沿着Parent向上更新出现次数,遇到lc=当前串的就停止。时间复杂度还不太会分析,待补。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 void add (int id,int c) int now=newnode (); maxlen[now]=maxlen[last]+1 ; cnt[now]=1 ; while (last && son[last][c]==0 ) son[last][c]=now,last=pre[last]; if (last) { int x=son[last][c]; if (maxlen[x]==maxlen[last]+1 ) pre[now]=x; else { int nq=newnode (); maxlen[nq]=maxlen[last]+1 ; memcpy (son[nq],son[x],sizeof (son[x])); pre[nq]=pre[x]; lc[nq]=lc[x];strval[nq]=strval[x]; pre[x]=pre[now]=nq; while (last && son[last][c]==x) son[last][c]=nq,last=pre[last]; } } else pre[now]=1 ; last=now; while (now && lc[now]!=id) { lc[now]=id; ++strval[now]; now=pre[now]; } } sam.init (); for (int i=1 ;i<=n;++i){ sam.last=1 ; scanf ("%s" ,s); for (int j=0 ;s[j];++j) sam.add (i,s[j]-'a' ); }
练习题目:
求字符串本质不同子串的个数 ,直接累加∣ s u b s t r i n g s ( s t ) ∣ \left|substrings(st) \right| ∣ s u b s t r i n g s ( s t ) ∣
1 2 3 4 5 6 7 ll count () ll ans=0 ; for (int i=1 ;i<=tot;++i) ans+=maxlen[i]-maxlen[pre[i]]; return ans; }
求两个串最长公共子串 ,对一个串建后缀自动机,另一个串在上面走,如果当前状态没有当前字符的转移,就沿着suffix link往回跳,很好理解。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 int LCS (char *s) int now=1 ,len=0 ,ans=0 ; for (int i=0 ;s[i];++i) { int x=s[i]-'a' ; if (son[now][x]) ++len,now=son[now][x]; else { while (now && son[now][x]==0 ) now=pre[now]; if (now==0 ) len=0 ,now=1 ; else len=maxlen[now]+1 ,now=son[now][x]; } ans=max (ans,len); } return ans; }
求一个串的第K小子串 ,T==0 表示不同位置的相同子串算作一个,T==1 则表示不同位置的相同子串算作多个。
还是先计算 e n d p o s endpos e n d p o s T==0,则每个状态cnt值都是1,如果 T==1,则还是和之前的代码一样,在suffix link构成的树上做拓扑排序,转移出cnt。
另外还需要知道从每个状态往后走会有多少种子串,记为 S u m [ x ] Sum[x] S u m [ x ]
S u m [ x ] = c n t [ x ] + ∑ i = 0 25 S u m [ s o n [ x ] [ i ] ] Sum[x]=cnt[x]+\sum_{i=0}^{25} Sum[son[x][i]]
S u m [ x ] = c n t [ x ] + i = 0 ∑ 2 5 S u m [ s o n [ x ] [ i ] ]
然后从根开始按照字典序dfs一下就可以求出第K小子串了。
给一个字符串S,求∑ 1 ≤ i < j ≤ n l e n ( T i ) + l e n ( T j ) − 2 l c p ( T i , T j ) \sum_{1\le i<j\le n} len(T_i)+len(T_j)-2lcp(T_i,T_j) ∑ 1 ≤ i < j ≤ n l e n ( T i ) + l e n ( T j ) − 2 l c p ( T i , T j ) T i T_i T i i i i l c p lcp l c p
把原串倒过来建后缀自动机,这样就把前缀变成了后缀。两个前缀的最长公共后缀是对应后缀自动机上两结点的LCA ,实上统计的话,枚举LCA做类似树dp的事情数一数即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 void addedge () for (int i=2 ;i<=tot;++i) e[pre[i]].push_back (i); } void dfs (int x) ll now=0 ; for (int i=0 ;i<e[x].size ();++i) { int y=e[x][i]; dfs (y); ans-=2LL *now*cnt[y]*maxlen[x]; now+=cnt[y]; } if (cnt[x]==1 ) ans-=2 *now*maxlen[x]; cnt[x]+=now; }
或者这样,类似容斥一下的统计
1 2 3 4 5 6 7 8 9 10 void dfs(int x) { for(int i=0;i<e[x].size();++i) { int y=e[x][i]; dfs(y); cnt[x]+=cnt[y]; } if(x!=1) ans-=1LL*cnt[x]*(cnt[x]-1)*(maxlen[x]-maxlen[pre[x]]); }
Alice和Bob玩游戏,有 n n n S i S_i S i t t t n n n t t t
显然是要在 t t t
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 int calc (char *s,int n) int now=1 ; for (int i=0 ;i<n;++i) now=son[now][s[i]-'a' ]; return ans[now]; } void work () for (int i=1 ;i<=tot;++i) for (int j=0 ;j<26 ;++j) if (son[i][j]) { e[son[i][j]].push_back (i); in[i]++; } int l=0 ,r=0 ; for (int i=1 ;i<=tot;++i) if (!in[i]) q[r++]=i; while (l!=r) { int x=q[l++]; int now=0 ; while (vis[x][now]) ++now; ans[x]=now; for (auto &y:e[x]) { vis[y][ans[x]]=true ; --in[y]; if (!in[y]) q[r++]=y; } } }
给一个串,求每个位置的最短识别子串的长度,最短识别子串定义是,在整个串中出现一次且覆盖到这个位置的最短的一个子串。
做法是找e n d p o s endpos e n d p o s 1 1 1