超实用！Stern-Brocot tree总结奉上

关于Stern-Brocot tree网上的资料较少（后记：实际上并不少，只是竞赛中讨论的不多），能够找到的资源有Wikipedia以及《具体数学》上的介绍，这里大概总结一下这个树形结构的性质。

Stern-Brocot tree:

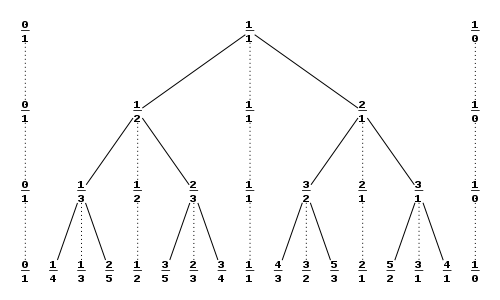
Stern-Brocot tree构成了一个无限的二叉排序树，可以将所有的正有理数从小到大列举出来。

构造方法可以理解为：先在左边写上$\frac{0}{1}$，右边写上$\frac{1}{0}$，代表零和正无穷，然后分子、分母分别相加，得到$\frac{1}{1}$，写在中间，之后每次把当前层复制到下一层，然后对于下一层相邻两个有理数之间还是分子分母分别相加，得到新的有理数，写在两者中间，重复这个操作就可以无限的写下去，进而得到所有的有理数。树形结构的获得见上图。

记树中的一个节点$\frac{y}{x}$，它是由$\frac{L_m}{L_n},\frac{R_m}{R_n}$这两个数产生的，那么可以发现：

1.$\frac{L_m}{L_n}$是位于左上方且离它最近的祖先，$\frac{R_m}{R_n}$是位于右上方且离它最近的祖先。

2.$gcd(x,y)=1$。

3.$R_mL_n-L_mR_n=1$。

4.以$\frac{y}{x}$为根的子树中的所有数都落在区间$(\frac{L_m}{L_n},\frac{R_m}{R_n})$中

找一个数$\frac{b}{a}$在树中的位置可以通过在树上二分，但如果一步一步走的话，时间复杂度关于a,b是线性的，比如找$\frac{1}{10^9}$，需要从根一直往左走$10^9-1$步。但是可以证明，在树上“拐弯”的次数是 $O(log)$ 的 ，可以与辗转相除法联系起来，详见这个视频。这样每次直走的步数我们可以列不等式$O(1)$求出，拐弯的过程递归下去就好了。也可以用具体数学书上的结论。

题目列表：

1.Alice, Bob, Oranges and Apples

题意：懒得叙述了，总之把在Stern-Brocot tree上走的过程抽象了一下，简化的题意就是给一个分数，输出从根到该点的路径。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main(){
    ll x,y;
    while(scanf("%lld%lld",&x,&y)!=EOF){
        if(__gcd(x,y)>1){
            puts("Impossible");
            continue;
        }
        while(x!=y){
            if(x<y) {
                ll t=(y-1)/x;
                y-=t*x;
                printf("%lldB",t);
            } else {
                ll t=(x-1)/y;
                x-=t*y;
                printf("%lldA",t);
            }
        }
        puts("");
    }
}

2. 2017 CCPC 哈尔滨 Cow`s Segment

题意：给两个高精度浮点数$a,b$，求最小的正整数$x$使得区间$[ax,bx)$包含整数（注，原题面有误，真实的数据是左闭右开的）。

思路：设$ax\le y<bx$，即$a\le \frac{y}{x}<b$，就按上面说的，在Stern-Brocot tree上二分，直到找到第一个符合条件的点，同时就是x的最小值。

(Java写起来太长了

import java.io.*;
import java.util.*;
import java.math.*;
public class Main
{
    final static BigInteger one=BigInteger.ONE;
    final static BigInteger zero=BigInteger.ZERO;
    final static BigInteger base=BigInteger.valueOf(10);
    final static int LEN=300;
    static BigInteger ans;
    public static BigInteger trans(String s){
        int len=s.length();
        int num=LEN,flag=0;
        BigInteger ans=BigInteger.valueOf(0);
        for(int i=0;i<len;++i)
        {
            if(s.charAt(i)=='.') flag=1;
            else 
            {
                num-=flag;
                int now=s.charAt(i)-'0';
                ans=ans.multiply(base).add(BigInteger.valueOf(now));
            }
        }
        for(int i=1;i<=num;++i)
            ans=ans.multiply(base);
        return ans;
    }
    public static void dfs(BigInteger a,BigInteger b,BigInteger c,BigInteger d,
    		BigInteger la,BigInteger lb,BigInteger ra,BigInteger rb,
    		BigInteger x,BigInteger y)
    {
        BigInteger le=b.multiply(x).subtract(a.multiply(y));
        BigInteger ri=d.multiply(x).subtract(c.multiply(y));
        if(le.compareTo(zero)<=0 && ri.compareTo(zero)>0)
        {
            ans=x;
            return ;
        }
        BigInteger k,tem;
        if(le.compareTo(zero)>0)
        {
            tem=a.multiply(rb).subtract(b.multiply(ra));
            k=le.add(tem.subtract(one)).divide(tem);
            dfs(a,b,c,d,
            x.add(k.subtract(one).multiply(ra)),y.add(k.subtract(one).multiply(rb)),
            ra,rb,
            x.add(k.multiply(ra)),y.add(k.multiply(rb)));
        }
        else
        {
            ri=ri.negate();
            tem=d.multiply(la).subtract(c.multiply(lb));
            k=ri.divide(tem).add(one);
            dfs(a,b,c,d,
            la,lb,
            x.add(k.subtract(one).multiply(la)),y.add(k.subtract(one).multiply(lb)),
            x.add(k.multiply(la)),y.add(k.multiply(lb)));
        }
    }
    public static void main(String[] args)
    {
        Scanner cin=new Scanner(System.in);
        BigInteger pow=base.pow(LEN);
        BigInteger a,b;
        int T=cin.nextInt();
        for(int cas=1;cas<=T;++cas)
        {
            String s=cin.next(),t=cin.next();
            a=trans(s);
            b=trans(t);
            dfs(pow,a,pow,b,one,zero,zero,one,one,one);
            System.out.println(ans);
        }
    }
}

3.Petrozavodsk Winter-2018. AtCoder Contest C Construct Point

题意：二维平面上给整点三角形的三个顶点坐标，判断三角形内部（不含边界）是否存在整点，如果有输出任意一个。

思路：先考虑这么一个子问题，在直线$y=\frac{b}{a}x$和$y=\frac{d}{c}x$之间找一个整点，范围$0<x\le D$，那么还是$\frac{b}{a}x < y<\frac{d}{c}x$，得到$\frac{b}{a}<\frac{y}{x}<\frac{d}{c}$，找到最小的x和D比较即可。对于任意三角形的话，通过分割，平移，对称的变换就能规约成上述子问题啦。

代码略。