题目来源NAIPC 2016 或 [Jsoi2016]最佳团体,你会发现这俩题完全一致…
(听说是那段时间jsoi就是汉化国外的题目)
题目链接:http://opentrains.snarknews.info/~ejudge/team.cgi?contest_id=006280
或https://nanti.jisuanke.com/t/A2026
或https://www.lydsy.com/JudgeOnline/problem.php?id=4753
题意是说有n+1个人,0号是CEO,1到n号是参选员工,每个员工i给一个薪水s和生产力p,还有一个推荐他的人的编号r(0≤r<i),现在要选出k个员工,如果选了某个员工那么他的推荐人也必须选(除非他的推荐人是CEO),使得选出k个员工的生产力之和除以薪水之和最大。
做法:n+1个人实际构成了一个树,CEO是根。首先01分数规划模型很显然,那么二分答案mid,新的点权为pi−si×mid,现在要求树上k+1个点的连通块(包括根)的最大点权和。
经典背包型dp,dp[i][j]表示以i为根的联通块大小为j的最大点权和,最后求出dp[0][k+1]小于0说明二分出来的值比答案大了,反之说明小了。
直观上看二维的状态,转移还需要枚举新加的一个子树选多少的点,这样似乎上是O(N3),会超时?
实际上,我们每次只for到子树大小,可以证明这样时间复杂度是O(N2)。直接看图理解吧:
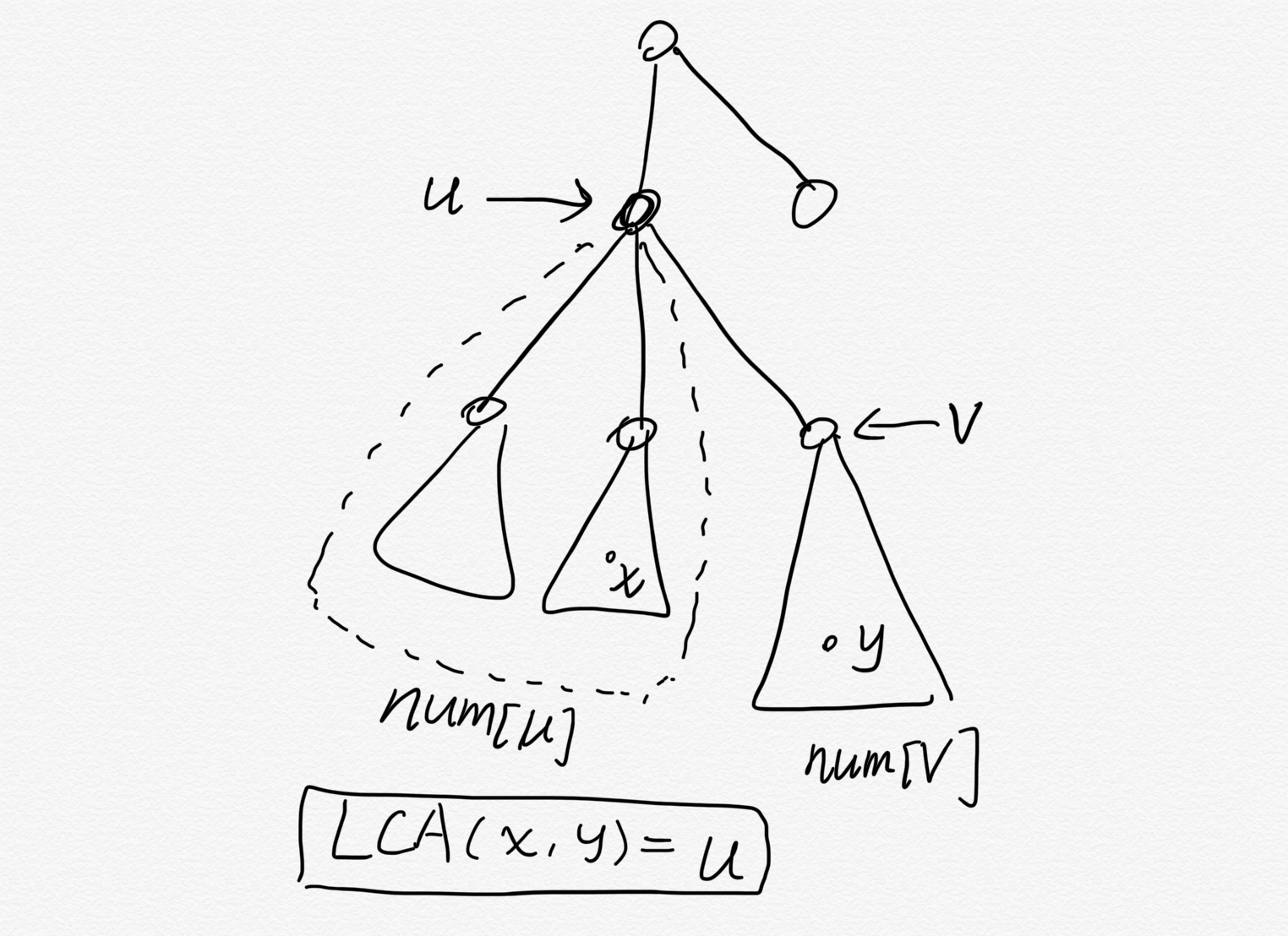
意思就是说这样的写法等价于枚举所有的点对(x,y)的时间。所以最终这道题的时间复杂度为O(N2logC)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| #include<bits/stdc++.h>
using namespace std;
#define N 2550
const double INF=1e99;
int k,n;
int num[N],a[N],b[N];
double dp[N][N],c[N],now[N];
vector<int> e[N];
void dfs(int u,int f)
{
double tmp[N];
tmp[0]=c[u];
num[u]=0;
for(auto &v:e[u])
{
if(v==f)continue;
dfs(v,u);
for(int i=0;i<=num[u]+num[v];i++)
now[i]=-INF;
for(int i=0;i<=num[u];i++)
for(int j=0;j<=num[v];j++)
now[i+j]=max(now[i+j],tmp[i]+dp[v][j]);
for(int i=0;i<=num[u]+num[v];i++)
tmp[i]=now[i];
num[u]+=num[v];
}
num[u]++;
dp[u][0]=0;
for(int i=1;i<=num[u];i++)
dp[u][i]=tmp[i-1];
}
double calc(double mid)
{
c[0]=0;
for(int i=1;i<=n;++i) c[i]=a[i]-mid*b[i];
dfs(0,-1);
return dp[0][k+1];
}
int main()
{
scanf("%d%d",&k,&n);
for(int i=1;i<=n;++i)
{
int fa;
scanf("%d%d%d",b+i,a+i,&fa);
e[fa].push_back(i);
}
double l=0,r=10000;
for(int i=1;i<=50;++i)
{
double mid=(l+r)/2;
if(calc(mid)>=0) l=mid;
else r=mid;
}
printf("%.3f\n",l);
return 0;
}
|
