基于Stern-Brocot tree的有理数集二分算法及其优化

0. 写在前面

本文中用 Stern-Brocot tree 做有理数二分的 idea 来自q神，后来我独立证明了其时间复杂度为 $O(\log{N})$ ，遂作此文，并作为算法课期末小论文提交（大概2020年的时候）。不知道竞赛圈中有没有类似的内容，或许本文是首创？在阅读之前，可以先看一下我以往创作的相关文章和视频：

另外本文可能有一些意识流的地方，写得并不严谨，请见谅。

1. 引言

二分法是算法研究中的一个极其重要的基础算法，或者说是一种重要的指导思想。比如，在有序数组中查找某一特定元素的位置或者判定其是否出现，或者数值分析中的求某一段单调函数的零点，又或者是在问题满足某种单调性时用二分枚举去代替暴力枚举，这样就将最优性问题转换成判定性问题，进而二分出最终答案。实际上，这类可以用二分算法解决的问题通常有一个相似的模型，然而对于解类型的不同，算法框架又稍有区别。一般来说，最常见的是在整数区间或实数区间上二分。然而对于某些问题，需要考虑的是在有理数集上二分，并将答案表示成最简分数的形式。这种情况下，二分更难实现，比如已知当前区间 $\left[ \frac{a}{b},\frac{c}{d}\right]$ ，如何求解当前区间的“中点”，从而对区间进行“二分”？借助数学工具Stern-Brocot tree可以完成这一任务。

Stern-Brocot tree是由德国数学家Moritz Stern和法国钟表匠Achille Brocot分别独立发现的。Stern-Brocot tree是一种展示所有正有理数的无限完全二叉树，其中树上节点与正有理数一一对应。它巧妙地将数论与数据结构联系在一起，构造过程十分优雅，且拥有众多神奇的性质。不仅如此，其与法里序列、连分数以及欧几里得算法等内容有着广泛而密切的联系。

本文第二节归纳总结了二分问题的共同点和算法的基本框架，并依据解类型的不同阐述了其中的区别。最后引出本文所讨论的问题——在有理数集中二分。

本文第三节重点介绍了Stern-Brocot tree的构造、性质以及相关证明。

本文第四节引入了Stern-Brocot tree中独特的数系，并将构造过程中的线性变换用矩阵乘积的形式来表示。最后从矩阵形式入手，解释了其与求最大公约数的欧几里得算法的联系。

本文第五节具体描述了在Stern-Brocot tree上实现对有理数集二分的算法，并逐步给出了优化。

2. 二分算法

考虑某问题在区间 $\left[ L,R \right]$ 中寻找答案 $a$ 。假设已知该问题在区间 $\left[L,a\right)$ 上有性质 $P$ ，在 $\left(a,R\right]$ 上不具有性质 $P$ ，且验证区间上任意一个点是否具有性质 $P$ 十分容易或者时间复杂度在可接受范围内，那么答案 $a$ 就可利用二分法求解。

这里说的性质 $P$ 是一种形象的说法，也可以理解为我们能通过简单的计算或是另外的算法来较快地询问二分中点与答案的大小关系。而区间能根据是否含有性质 $P$ 分成前后两段通常是由某种单调性决定的。

2.1. 整数集上的二分

当只考虑区间中的整点时，即二分的对象为一段连续的整数时，情况最简单。假设在 $a$ 点处具有性质 $P$ ，则伪代码如下所示：

\begin{algorithm}
\caption{BinarySearchForInteger} 
\begin{algorithmic}
\PROCEDURE{BinarySearchForInteger}{$L,R$}
\WHILE{$L\lt R$}
    \STATE  $mid \gets \lceil (L+R)/2 \rceil$
    \IF{\Call{HasProperty}{$mid$}} 
    	\STATE $L \gets mid$
    \ELSE 
    	\STATE $R \gets mid-1$
    \ENDIF
\ENDWHILE
\RETURN $L$
\ENDPROCEDURE
\end{algorithmic}
\end{algorithm}

若在 $a$ 点处不具有性质 $P$ ，则在取整及加减一稍有区别，情况类似。

假设每次验证的时间为 $O(1)$ ，由于搜索的区间长度 $n$ 每次会减少一半，所以二分的时间复杂度 $O(\log{n})$ 。举个例子，在有序数组 $A[1\dots n]$ 中二分查找某元素 $y$ 的位置，这里假设数组元素严格单调递增，且 $y$ 一定存在。那么初始区间即 $\left[1,n\right]$ ，代表下标。上述所说的性质 $P$ 在这里即为“该位置的数组元素小于等于 $y$ ”。

2.2. 实数集上的二分

然而对于一些数值分析或是计算几何之类的问题来说，需要的答案 $a$ 往往是浮点数类型，是一定精度内的近似解，比如要求精确到小数点后六位，或者要求绝对误差限或相对误差限不超过一个设定好的且足够小的 $\epsilon$ 值。这样循环终止条件可以根据不同的精度需求自行设定。若初始区间长度为 $n$ ，则时间复杂度为 $O(\log{(n/\epsilon)})$ ，所需精度越高， $\epsilon$ 就需要设定的越小，时间代价就越大。

由于是浮点数，代码实现时则无需考虑 $a$ 点处是否也具有性质 $P$ 。

\begin{algorithm}
\caption{BinarySearchForReal} 
\begin{algorithmic}
\Procedure{BinarySearchForReal}{$L,R$}
\While{$R-L>eps$}
\State  $mid \gets (L+R)/2$
\If{\Call{HasProperty}{$mid$}} 
\State $L \gets mid$
\Else 
\State $R \gets mid$
\EndIf
\EndWhile
\Return $L$
\EndProcedure
\end{algorithmic}
\end{algorithm}

例如，求解 $f(x)=x^2-2$ 在区间 $\left[0,2\right]$ 上的零点，性质 $P$ 则为“ $f(x)<0$ ”。

2.3. 有理数集上的二分

对于有理数的情况我们也可以抽象出类似的问题。考虑在有理数集 $Q_N= \left\{ \frac{p}{q}:p,q\in \left\{ 1,2,\dots,N\right\} \right\}$ 上确定未知数 $\frac{x}{y}$ 。已知在 $(0,\frac{x}{y}]$ 上有性质 $P$ ，在 $(\frac{x}{y},+\infty)$ 上不具有性质 $P$ ，且可以用 $O(1)$ 的时间询问任一有理数 $\frac{p}{q}$ 是否具有性质 $P$ ，换句话说，可以很快判断出 $\frac{p}{q}$ 是否小于等于答案 $\frac{x}{y}$ 。目标就是用尽量少的询问次数确定 $\frac{x}{y}$ 。

这样定义问题的好处是规定了分子分母的上界，那么只需考虑 $O(N^2)$ 个不同的有理数。定义这样的有理数集 $Q_N$ 也相当于规定了求解的精度要求， $N$ 越大代表精度越高。可以看到，有理数集上的二分问题比之前讨论过的整数集、实数集上的二分要难。

一个典型应用是在直角坐标系第一象限上二分斜率大小。将斜率表示成最简分数的形式避免了浮点数计算带来的精度损失，从而方便处理一些整点相关的问题。该问题模型也可以用来做无理数的最佳有理逼近。

3. Stern-Brocot tree

在解决有理数集上二分问题之前，先介绍一下Stern-Brocot tree。在本节中将给出Stern-Brocot tree的构造过程以及相关性质的证明。

3.1. Stern-Brocot tree的构造

首先定义两个分数的中位分数：

定义 1（中位分数）. 两个分数 $\frac{a}{c}$ 和 $\frac{b}{d}$ 的中位分数为 $\frac{a+b}{c+d}$ 。

后面会看到在有理数集上二分时，我们会使用中位分数来作为每次二分的“中点”。

有了中位分数的概念就可以开始构造Stern-Brocot tree了。我们先来构造树上每层的分数序列，构造从两个分数 $\frac{0}{1},\frac{1}{0}$ 出发，作为第 $0$ 层。第一个数是 $0$ ，而第二个数实际上并不是严格意义上的分数，这里将其看成无穷大即可。

每次将相邻两分数的中位分数插在它们的中间，一层一层无限地计算下去，那么前几层就会得到：

\frac{0}{1},\bm{\frac{1}{1}},\frac{1}{0}

\frac{0}{1},\bm{\frac{1}{2}},\frac{1}{1},\bm{\frac{2}{1}},\frac{1}{0}

\frac{0}{1},\bm{\frac{1}{3}},\frac{1}{2},\bm{\frac{2}{3}},\frac{1}{1},\bm{\frac{3}{2}},\frac{2}{1},\bm{\frac{3}{1}},\frac{1}{0}

可以看到，第一次产生 $1$ 个新值，第二次产生 $2$ 个，第三次产生4个，再接下来会新得到8个值，以此类推。不难发现，一个在某层中新产生的分数会在下一层的计算中产生左右两个新的分数，那么让 $\frac{1}{1}$ 为根，每层中的新值分别向下一层与其相邻的左右两个点连边，并作为其的两个孩子节点，这样就构造出了如图一所示的Stern-Brocot tree（实线连接的树）。假设某分数 $\frac{a+c}{b+d}$ 由 $\frac{a}{b}$ 和 $\frac{c}{d}$ 构造得到，那么可以发现， $\frac{a}{b}$ 在树中是 $\frac{a+c}{b+d}$ 节点从下往上看第一个小于其值的祖先节点，即它左上方最近的祖先。类似地， $\frac{c}{d}$ 是 $\frac{a+c}{b+d}$ 右上方最近的祖先。

事实上，Stern-Brocot tree不仅是一个无限完全二叉树，其也满足二叉搜索树的性质：每个点的权值大于等于左子树中任意一点的权值，并且小于等于右子树任意一点的权值。当然，等于的情况在这里并不会出现。若只考虑这个无限大的树的前 $k$ 层，对其做中序遍历，并将 $\frac{0}{1}$ 和 $\frac{1}{0}$ 分别添加在序列的头尾，那么就得到了我们之前构造的第 $k$ 层序列。

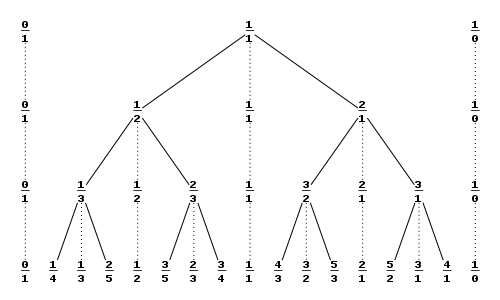
3.2. Stern-Brocot tree的性质

为了说明Stern-Brocot tree能展示所有的正有理数且树上节点与正有理数一一对应，主要需证明以下三条性质：有序性、不可约性、所有正有理数的存在性。

3.2.1. 有序性

定理1. 若 $\frac{a}{c}<\frac{b}{d}$ 且 $a,b,c,d\ge 0$ ，则 $\frac{a}{c}<\frac{a+b}{c+d}<\frac{b}{d}$ 。

这条性质是说两分数的中位分数的大小严格介于它们中间，经过简单的移项通分即可证明，此处略去。因为第 $0$ 层的分数是升序排列的，因此每次将相邻两分数的中位分数写在中间不会破坏每层的有序性。

3.2.2. 不可约性

定理2. 若 $\frac{a}{b}$ 和 $\frac{c}{d}$ 是构造过程中任意一层的相邻分数，那么就有 $bc-ad=1$ 。

证明. 初始第 $0$ 层是正确的， $1\times 1-0\times 0 =1$ 。当插入中位分数后，序列变成了

\dots,\frac{a}{b},\frac{a+c}{b+d},\frac{c}{d},\dots

需要检验的新情形是

\begin{aligned} b(a+c) - a(b+d) &= 1 \\ c(b+d) - d(a+c) &= 1 . \end{aligned}

根据 $bc-ad=1$ 不难证明其正确性。

得到该性质之后，结合裴蜀定理，即关于未知数 $x$ 和 $y$ 的线性不定方程 $Ax+By=C$ 有整数解，当且仅当 $C$ 是 $gcd(A,B)$ 的倍数，可以推出 $gcd(a,b)=gcd(c,d)=1$ ，即构造出的任意分数都是最简分数。

3.2.3. 所有正有理数的存在性

根据有序性可以得知，一个分数在树中不会出现超过一次。更进一步，可以证明：

定理3. 任何满足 $gcd(x,y)=1$ 的正有理数 $\frac{x}{y}$ 都能通过有限步构造得到。

证明. 一开始我们有

\frac{a}{b}=\frac{0}{1}<\frac{x}{y}<\frac{1}{0}=\frac{c}{d}

每次比较 $\frac{x}{y}$ 和 $\frac{a+c}{b+d}$ ，分为三种情况，并不断进行下去：

$\frac{x}{y}=\frac{a+c}{b+d}$ ，则构造出了 $\frac{x}{y}$ ；
$\frac{x}{y}<\frac{a+c}{b+d}$ ，则令 $c\gets a+c$ ， $d\gets b+d$ ；
$\frac{x}{y}>\frac{a+c}{b+d}$ ，则令 $a\gets a+c$ ， $b\gets b+d$

那么就有

\begin{aligned} \frac{x}{y} - \frac{a}{b} &>0 \\ \frac{c}{d} - \frac{x}{y} &>0 \end{aligned}

\begin{aligned} bx - ay &\ge 1 \\ cy - dx &\ge 1 \end{aligned}\tag{1,2}

(1)乘上 $c+d$ ，(2)乘上 $a+b$ ，然后两式相加得到

\begin{aligned} (c+d)(bx - ay) + (a+b)(cy - dx) \ge a+b+c+d \end{aligned} \tag{3}

根据定理 2 化简可得

\begin{aligned} x+y \ge a+b+c+d \end{aligned}\tag{3}

因为每一步中 $a,b,c,d$ 里至少有一个变量会变大，所以(3)式不会一直成立。也就是说，一定能在有限步内构造出 $\frac{x}{y}$ 。

这样所有正有理数都会在树中出现且仅出现一次。实际上，这个证明过程本质就是在Stern-Brocot tree这个二叉搜索树上去二分地定位一个正有理数的位置，后文还会涉及到类似内容。

4. 准备工作

上一节证明了树上节点与正有理数是一一对应的，本节将引入Stern-Brocot tree独特的数系来具体阐明这个一一对应的关系。之后用矩阵的形式描述从根节点往下移动的过程中分子分母的变化。本节最后将揭示Stern-Brocot tree与求两个数最大公约数的欧几里得算法的联系，为第 $5$ 节给出的优化提供理论基础。

4.1. 数系的引入

在上一小节中，我们已经知道了所有正有理数都会在树中的某个位置恰好出现一次。考虑用 L 或 R 表示从根走到某节点的路径时每次往左孩子还是右孩子走，那么这样一个由 L 和 R 组成的有限长度的字符串就唯一确定了树上的一个位置，也就唯一表示了一个正有理数。例如 LRL，表示从根 $\frac{1}{1}$ 往左走到 $\frac{1}{2}$ ，然后往右走走到 $\frac{2}{3}$ ，再往左到 $\frac{3}{5}$ ，所以 LRL 表示分数 $\frac{3}{5}$ 。特殊的，根节点 $\frac{1}{1}$ 对应一个空字符串，用字符 $I$ 表示。

定义2. 若 $S$ 是由 L 和 R 组成的字符串， $\frac{x}{y}$ 为Stern-Brocot tree上与 $S$ 对应的分数，则定义
$\begin{aligned} f(S) = \frac{x}{y} \end{aligned}$

定理4. 若 $f(S)=\frac{x}{y}$ ，则字符串 $S$ 的长度不会超过 $x+y-2$ 。

根据定理 3 证明中的(3)式即可证明。特殊地，当 $\frac{x}{y}$ 为 $\frac{1}{n}$ 或 $\frac{n}{1}$ 的形式时， $S$ 长度为 $n-1$ ，此时达到最长。这个性质说明直接按照定理 3 证明中的二分方法去定位 $\frac{x}{y}$ 的话，时间复杂度是线性的，需要发掘Stern-Brocot tree更多更加本质的特点，从而达到优化。

4.2 矩阵表示

在 3.2.3 小节证明的二分过程中，我们维护了四个变量 $a,b,c,d$ 并做了一些线性的变换，本节中用 $2\times 2$ 矩阵来描述同样的过程。

定义3. 假设某分数 $\frac{a+c}{b+d}$ 由 $\frac{a}{b}$ 和 $\frac{c}{d}$ 构造得到，其中 $\frac{a}{b}$ 是它左上方最近的祖先， $\frac{c}{d}$ 是它右上方最近的祖先，且 $f(S)=\frac{a+c}{b+d}$ ，定义矩阵：
$\begin{aligned} M(S)= \begin{pmatrix} b & d \\ a & c \end{pmatrix} \end{aligned}$

注意，这里将祖先分数的分子放在了分母的下方，好处是根节点可以表示成一个单位矩阵，即

\begin{aligned} M(I)= \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \end{aligned}

根的左右孩子 $\frac{1}{2}$ 和 $\frac{2}{1}$ 分别表示为

\begin{aligned} M(L)= \begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix},\, M(R)= \begin{pmatrix} 1 & 0 \\ 1 & 1 \end{pmatrix} \end{aligned}

考虑证明 3.2.2 二分的后两种情况，即走到 $\frac{a+c}{b+d}$ 的左右孩子

\begin{aligned} M(SL)= \begin{pmatrix} b & b+d \\ a & a+c \end{pmatrix},\, M(SR)= \begin{pmatrix} b+d & d \\ a+c & c \end{pmatrix} \end{aligned}

不难发现

\begin{aligned} M(SL) & = \begin{pmatrix} b & b+d \\ a & a+c \end{pmatrix}= \begin{pmatrix} b & d \\ a & c \end{pmatrix} \begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix} \\ M(SR) & = \begin{pmatrix} b+d & d \\ a+c & c \end{pmatrix} = \begin{pmatrix} b & d \\ a & c \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 1 & 1 \end{pmatrix} \end{aligned}

一般地，下述定理成立

定理5. 设 $S,T$ 是两个由 L 和 R 组成的字符串，则
$\begin{aligned} M(ST)=M(S)M(T) \end{aligned}$

因此我们可以将 LR 字符串代表的路径写成一系列 $M(L)$ 和 $M(R)$ 矩阵连乘的结果。

4.3. 欧几里德算法

考虑简化上述二分方法，若已知分数 $\frac{x}{y}$ ，对应的矩阵表示为 $\begin{pmatrix} b & d \\ a & c \end{pmatrix}$ ，那么有 $x=a+c$ 和 $y=b+d$ 。假设 $x>y$ ，那么对应在树上的路径第一步必为 R，设剩余路径为 $S$ ，则有 $f(RS)=\frac{x}{y}$ 。

即

\begin{aligned} \begin{pmatrix} 1 & 0 \\ 1 & 1 \end{pmatrix} M(S)=\begin{pmatrix} b & d \\ a & c \end{pmatrix} \end{aligned}

解得

\begin{aligned} M(S)=\begin{pmatrix} 1 & 0 \\ -1 & 1 \end{pmatrix}\begin{pmatrix} b & d \\ a & c \end{pmatrix}=\begin{pmatrix} b & d \\ a-b & c-d \end{pmatrix} \end{aligned}

因此

\begin{aligned} f(S)=\frac{(a+c)-(b+d)}{b+d}=\frac{x-y}{y} \end{aligned}

同理，若 $x<y$ ，设 $f(LS)=\frac{x}{y}$ ，则有 $f(S)=\frac{x}{y-x}$ 。这样假设我们已知 $\frac{x}{y}$ ，想求出它在树上的位置，即对应的字符串序列，那么每次可以分两种情况：当 $x>y$ 时，输出一个 R，并令 $x$ 减去 $y$ ；当 $x<y$ 时，输出一个 L，并令 $y$ 减去 $x$ 。反复执行上述流程，直到 $x=y=1$ 结束，此时输出的字符串就是答案。实际上，这个过程就是对 $x$ 和 $y$ 做辗转相减，因为 $x$ 和 $y$ 互质，所以最终一定有 $x=y=1$ 。

这样，我们自然可以将其优化成辗转相除法。如下所示，代码 $LOCATE(x,y)$ 作用即输出 $\frac{x}{y}$ 的路径表示，只是这次对于同一段连续的 L 或连续的 R，只输出一个字符和其连续出现的次数。

\begin{algorithm}
\caption{Locate}
\begin{algorithmic}
\Procedure{Locate}{$x,y$}
\While{$x\ne y$}
\If{$x\le y$} 
\State $step \gets \lfloor (y-1)/x \rfloor $
\State $y \gets y-step\times x$
\State \PRINT $\text{'L'},step$
\Else 
\State $step \gets \lfloor (x-1)/y \rfloor $
\State $x \gets x-step\times y$
\State \PRINT $\text{'R'},step$
\EndIf
\EndWhile
\EndProcedure
\end{algorithmic}
\end{algorithm}

其中，第 4 行和第 8 行中的减一是为了避免最后一次while循环将 $x$ 或 $y$ 减小至0，所以除了最后一次除法外，在树上定位 $\frac{x}{y}$ 的过程与求 $x$ 和 $y$ 最大公约数的欧几里德算法步骤完全相同。根据拉梅定理， $x$ 和 $y$ 辗转相除的步数不超过 $min(x,y)$ 十进制位数的 $5$ 倍。由此可以得出该算法的时间复杂度为 $O(\log{(x+y)})$ 。

5. Stern-Brocot tree上的二分算法及其优化

有了之前的准备工作，在这一节中将解决 2.3 小节中提出的有理数集上的二分问题。需要注意的是，该问题与 4.3 小节中的定位问题是不同的。主要区别在于有理数集上的二分问题中 $\frac{x}{y}$ 是未知的，需要通过二分地询问从而逐步确定，而 4.3 小节所讨论的是已知一有理数 $\frac{x}{y}$ 去找它在树中的位置。

一个直接的方法是将所有可能的 $O(N^2)$ 个有理数列出来，排序后利用整数区间上二分的模型，虽然二分的复杂度是 $O(\log{N})$ ，但是预处理的过程就已经需要 $O(N^2)$ 的时间和空间了。[2]提出了一种 $O(\log{N})$ 的算法，先用指数搜索的技巧确定答案的整数部分，然后用一种本质为连分数展开的递归方法确定小数部分。本文提出的方法时间复杂度同样为 $O(\log{N})$ ，并且也使用了指数搜索，不同的是本文提出的方法是非递归的，且没有分别计算整数与小数部分，而是在一个大的二分查找框架中确定答案，思路是寻求Stern-Brocot tree与欧几里德算法的联系。

5.1. 朴素的二分方法

考虑每次在树上从根出发一步一步地走，询问当前分数 $\frac{p}{q}$ 是否小于等于答案。若是，则更新答案为当前分数，并走到右孩子上；若否，则直接走到左孩子上。当 $p>N$ 或 $q>N$ 时，算法停止，此时答案记录的分数即为我们想要的结果。根据定理4可知，这种方法的时间复杂度是 $O(N)$ 。

5.2. 二分优化

根据 4.3 节可得出以下结论：

定理 6. 设 $f(S)=\frac{x}{y}$ ，若字符串中连续相同的字符为一段，则字符串 $S$ 的段数是 $O(\log{(x+y)})$ 的。换句话说，从根节点到 $\frac{x}{y}$ 的路径拐弯的次数是 $O(\log{(x+y)})$ 的。

那么考虑将朴素二分过程的一步一步走改成一段一段走，对于每一段，再次二分步长从而走到下一个“拐点”上。因为每次的步长未知，所以二分的上界设为 $N$ 。这样，因为有 $O(\log{N})$ 段，对于每段又需要分别做一次 $O(\log{N})$ 的二分，所以该方法的时间复杂度为 $O(\log^2{N})$ 。

5.3. 进一步优化

直觉上来说，该方法还有进一步优化的空间。思考一下树上路径的特点，如果段数少，则每一段步长就可能会很长，比如形如 $\frac{1}{n}$ 这样的分数， $LLLLL\dots$ ;如果段数多，则每一段步长就会很短，比如斐波那契数列相邻两项之比， $LRLRLR\dots$ 。因此，在之前优化中二分上限如果不是每次跑满 $O(\log{N})$ ，而是 $O(\log{s_i})$ 的话（假设 $s_i$ 是第 $i$ 段的长度），时间复杂度就可能降下来。

这里要用到指数搜索，即先倍增后二分的技巧。一开始先倍增的跳，跳 $1$ 步， $2$ 步， $4$ 步， $8$ 步…直到 $2^j$ 步时判断出已经跳过了拐点，之后即可确定 $2^{j-1}\le s_i <2^j$ ，那么再在区间 $\left[2^{j-1},2^j\right)$ 上二分步长即可，显然最多只需询问 $2\log{s_i}+O(1)$ 次，第 $i$ 次倍增后二分的时间复杂度就是 $O(\log{s_i})$ 。伪代码如下：

\begin{algorithm}
\caption{BinarySearchForRational} 
\begin{algorithmic}
\Procedure{BinarySearchForRational}{}
\State $a,b,c,d \gets 0,1,1,0$
\While{$a+c\le N \textbf{ and } b+d\le N$}
	\If{\Call{HasP}{$a+c,b+d$}}
		\State $step  \gets 1$
		\While{$a+step\times c\le N \textbf{ and } b+step\times d\le N \textbf{ and } $\Call{HasP}{$a + step \times c, b + step \times d$}}
			\State $step \gets step\times 2$
		\EndWhile
		\State $ L,R \gets \lfloor step/2\rfloor ,step - 1$
		\While{$L\lt R$}
			\State $mid \gets \lceil (L + R) / 2\rceil$
			\If{\Call{HasP}{$a + mid \times c, b + mid \times d$}}
				\State $L \gets mid$
			\Else 
				\State $R \gets mid-1$
			\EndIf
		\EndWhile
		\State $a,b \gets a+L\times c,b+L\times d$
		\State $ansx,ansy= a,b$
	\Else 
		\State $step  \gets 1$
		\While{$step\times a+ c\le N \textbf{ and } step\times b+ d\le N \textbf{ and } \textbf{ not } $\Call{HasP}{$step \times a +  c, step \times b +  d$}}
			\State $step \gets step\times 2$
		\EndWhile
		\State $ L,R \gets \lfloor step/2\rfloor +1 ,step$
		\While{$L \lt R$}
			\State $mid \gets \lfloor (L + R) / 2\rfloor$
			\If{\Call{HasP}{$mid \times a +  c, mid \times b + d$}}
				\State $R \gets mid$
			\Else 
				\State $L \gets mid+1$
			\EndIf
		\EndWhile
		\State $c,d \gets (L-1)\times a+c,(L-1)\times  b+d$
	\EndIf
\EndWhile
\Return $ansx,ansy$
\EndProcedure
\end{algorithmic}
\end{algorithm}

后面考虑如何证明总的时间复杂度为 $O(\log{N})$ 。

设 $r_0=x,r_1=y$ ，不妨设 $x\ge y$ ，由辗转相除得到一系列式子：

\begin{aligned} &r_0 =q_1r_1+r_2,\\ &r_1 =q_2r_2+r_3,\\ & \dots,\\ &r_{k-2}=q_{k-1}r_{k-1}+r_k,\\ &r_{k-1}=q_kr_k \end{aligned}

其中 $k$ 表示 $x$ 和 $y$ 做辗转相除的除法次数，也是 Stern-Brocot tree 上，根节点到 $\frac{x}{y}$ 的路径段数。根据 4.3 小节可知， $s_i=q_i(1\le i <k),s_k=q_k-1$ ，即第 $i$ 段路径的长度等于辗转相除中每次得到的商，除了最后一段是 $q_k-1$ 。

由于询问只能查询当前有理数是否小于等于答案，因此在树上二分查找的过程中遇到最终答案并记录后也不会立刻停止算法，而是会再往右走一步，之后一直向左走，直到分子或分母超过 $N$ 。到节点 $\frac{x}{y}$ 之后，从右侧不断往左逼近 $\frac{x}{y}$ 的步数不超过 $\frac{N}{x}$ 。因此，方法三的总询问次数可以分到达 $\frac{x}{y}$ 之前与之后这两段计算：

\begin{aligned} &\sum_{i=1}^{k}(2\log{s_i}+O(1)) + 2\log{\frac{N}{x}}+O(1) \\ \le& 2\sum_{i=1}^{k}\log{q_i}+ 2\log{N}-2\log{x} +O(\log{x})\\ =&2\sum_{i=1}^{k}\log{\lfloor\frac{r_{i-1}}{r_i}\rfloor}+ 2\log{N}-2\log{x}+O(\log{x})\\ \le & 2\sum_{i=1}^{k}\log{\frac{r_{i-1}}{r_i}}+ 2\log{N}-2\log{x}+O(\log{x})\\ =& 2\log{\prod_{i=1}^{k}\frac{r_{i-1}}{r_i}}+ 2\log{N}-2\log{x} +O(\log{x})\\ =&2\log{\frac{r_{0}}{r_n}}+ 2\log{N}-2\log{x}+O(\log{x})\\ =&2\log{x}+ 2\log{N}-2\log{x}+O(\log{x})\\ =&O(\log{N}) \end{aligned}

所以最终本文实现了在 $O(\log{N})$ 时间内通过询问某个数是否小于等于答案的方式在有理数集 $Q_N= \left\{ \frac{p}{q}:p,q\in \left\{ 1,2,\dots,N\right\} \right\}$ 上确定未知数 $\frac{x}{y}$ 。该方法用非递归方法实现，借助Stern-Brocot tree的结构来实现对有理数的二分，二分时每次通过指数搜索快速走到路径拐点，并结合欧几里得算法证明了该算法是对数时间的。根据信息论理论，该复杂度达到了理论下界。至此，问题解决。

参考文献

[1] Graham R L, Knuth D E, Patashnik O, et al. Concrete mathematics: a foundation for computer science[J]. Computers in Physics, 1989, 3(5): 106-107.

[2] Kwek S, Mehlhorn K. Optimal search for rationals[J]. Information Processing Letters, 2003, 86(1): 23-26.

[3] Bentley J L, Yao A C C. An almost optimal algorithm for unbounded searching[J]. Information processing letters, 1976, 5(SLAC-PUB-1679).